A Theory of Information Systems

This chapter documents a theory of information systems, upon which Ampersand generates information systems.

The purpose of an information system is to make data meaningful to its users. Users have their own tasks and responsibilities and may work from different locations and on different moments. This collective use by multiple users serves a purpose which we will loosely call "the business". To preserve meaning, the business maintains semantic constraints on the data, amidst of all changes that are going on around them.

Information systems are typically used by actors (both users and computers) who are distributed and work with data all the time. As a consequence, the data in a system changes continually. In practice, actors "talk to" the system through an ingress mechanism, which connects each user to the right interface(s). The ingress function is provided by the deployment platform, so it is beyond the scope of this paper. Also, every interface runs independent of other interfaces, meaning that each interface can be stopped, (re)started and substituted without disrupting the other interfaces.

Every system contains a dataset, which represents the state of the system. Every interface produces and consumes events that may change the state of the system. This state is represented in a persistent store, aka the database. Events that the system detects may cause the state to change.

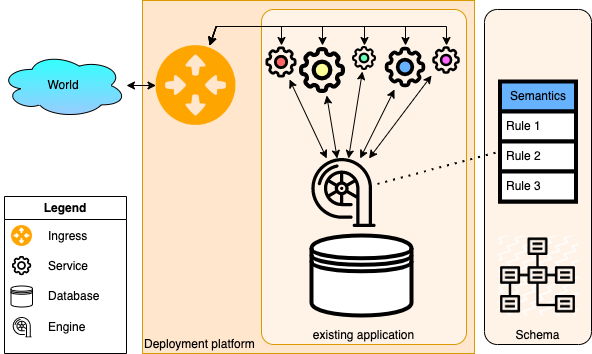
To keep our theory technology independent, datasets are assumed to contain triples. This makes the theory valid for any kind of database that triples can represent, such as SQL databases, object-oriented databases, graph databases, triple stores, and other no-SQL databases. The system's semantics is represented as constraints, which most database management systems refer to as integrity rules. The purpose of integrity rules is to keep the constraints they represent satisfied.

An information system is a combination of dataset, schema, and functionality. Each is defined in a separate section.

Datasets

A dataset $\mathscr{D}$ describes a set of structured data, which is typically stored persistently in a database of some kind. The notation $\mathscr{D}_{\mathscr{S}}$ refers to the dataset of a particular information system $\mathscr{S}$. The purpose of a dataset is to describe the data of a system at one point in time. Before defining datasets, let us first define the constituent notions of atom, concept, relation, and triple.

Atoms serve as data elements. Atoms are values without internal structure of interest, meant to represent atomic data elements (e.g. dates, strings, numbers, etc.) in a database. From a business perspective, atoms represent concrete items of the world, such as Peter, 1, or the king of France. By convention throughout the remainder of this paper, variables $a$, $b$, and $c$ represent atoms. All atoms are taken from an infinite set called $\mathbb{A}$.

Concepts are names that group atoms of the same type. All concepts are taken from an infinite set $\mathbb{C}$. $\mathbb{C}$ and $\mathbb{A}$ are disjoint. For example, a developer might choose to classify Peter and Melissa as Person, and 074238991 as a TelephoneNumber. In this example, Person and TelephoneNumber are concepts. In the sequel, variables $A$, $B$, $C$, $D$ will represent concepts.

The relation $\text{\it inst}:\mathbb{A}\times\mathbb{C}$ is the instance relation between atoms and concepts. The expression $a\ \text{\it inst}\ C$ means that atom $a$ is an instance of concept $C$. This relation is used in the type system, in which $\text{\it inst}$ assigns a concept to every atom in the dataset.

Relations serve to organize and store data, to allow a developer to represent facts. In this paper, variables $r$, $s$, and $d$ represent relations. All relations are taken from an infinite set $\mathbb{R}$. $\mathbb{R}$ is disjoint from $\mathbb{C}$ and $\mathbb{A}$. Every relation $r$ has a name, a source concept, and a target concept. The notation $r=\text{\it n}_{\langle{A},{B}\rangle}$ denotes that relation $r$ has name $n$, source concept $A$, and target concept $B$.

Triples serve to represent data. A triple is an element of $\mathbb{A}\times\mathbb{R}\times\mathbb{A}$.

A dataset $\mathscr{D}$ is a tuple $\langle{\mathcal{T}},{\text{\it inst}}\rangle$ that satisfies:

$\forall\langle{a},{\text{\it n}_{\langle{A},{B}\rangle}},{b}\rangle\in\mathcal{T}:\ a\ \text{\it inst}\ A\ \wedge\ b\ \text{\it inst}\ B$

This equation defines what it means for a triple to be well-typed. For example, $\langle{\text{{\tt\small Peter}}},{\text{\it phone}_{\langle{\tt Person},{\tt TelephoneNumber}\rangle}},{\text{{\tt\small 074238991}}}\rangle$ is a triple. The equation says that Peter is an instance of Person and 074238991 is an instance of TelephoneNumber. In practice, users can say that Peter has telephone number 074238991. So, the "thing" that Peter refers to (which is Peter) has 074238991 as a telephone number. This "meaning from practice" has no consequences in the formal world. Users are entirely free to attach a practical meaning to a triple.

The notations $\mathcal{T}_{\mathscr{D}}$ and $\text{\it inst}_{\mathscr{D}}$ are used to disambiguate $\mathcal{T}$ and $\text{\it inst}$ when necessary. Every dataset is an element of an infinite set called $\mathbb{D}$. To save writing in the sequel, the notation $a\ r\ b$ means that $\langle{a},{r},{b}\rangle\in\mathcal{T}$.

A relation $r$ can serve as a container of pairs, as defined by the function $\text{\it pop}_r:\mathbb{D}\rightarrow\cal{P}\{\mathbb{A}\times\mathbb{A}\}$. It defines a set of pairs, also known as the population of $r$:

$\text{\it pop}_{r}(\mathscr{D})\ =\ \{ \langle{a},{b}\rangle\mid\ \langle{a},{r},{b}\rangle\in\mathcal{T}_{\mathscr{D}}\}$

So, for every dataset $\mathscr{D}$:

$\langle{a},{b}\rangle\in\text{\it pop}_{\text{\it n}_{\langle{A},{B}\rangle}}(\mathscr{D})\ \Rightarrow\ a\ \text{\it inst}\ A\ \wedge\ b\ \text{\it inst}\ B$

For a developer, this means that the type of an atom depends only on the relation in which it resides; not on the actual population of the database. This allows for static typing, which has well established advantages for the software engineering process [@HanenbergKRTS14; @Petersen2014].

Schemas

To design an information system, a developer defines a schema in which she defines concepts, relations, and rules. Together, the concepts, relations, and rules capture the semantics of an information system [@Spivak2012]. Each rule in a schema serves to constrain the dataset, to ensure its semantic integrity. Every rule is an element of an infinite set called $\mathbb{U}$, which is disjoint from $\mathbb{A}$, $\mathbb{C}$, $\mathbb{R}$, and $\mathbb{D}$. In this paper, variables $u$ and $v$ represent rules.

A type system in Ampersand [@vdWoude2011] identifies certain rules that are provably false. It also ensures that all rules can be interpreted within the set of relations in the schema. Due to this type system, the Ampersand compiler only generates code for scripts without type errors. As a result, for every rule $u$ in the schema, there is a predicate $\text{\it sat}_{u}(\mathbb{D})$ that says whether dataset $\mathscr{D}$ satisfies rule $u$. A discussion of the type system is out of scope because this paper only makes use of the predicate $\text{\it sat}_{u}(\mathbb{D})$.

Rules serve as invariants, i.e. constraints that the data in the database must satisfy at all times. At times in which the dataset does not satisfy a rule, that rule is said to be broken. In those cases, something or someone must take action to fix the situation and restore invariance of that rule.

A schema $\mathscr{Z}$ is a triple $\langle{\mathcal{C}},{\mathcal{R}},{\mathcal{U}}\rangle$, in which $\mathcal{C}$ is a finite set of concepts, $\mathcal{R}$ is a finite set of relations, and $\mathcal{U}$ is a finite set of rules. The notation $\mathscr{Z}_{\mathscr{S}}$ refers to the schema of information system $\mathscr{S}$. Disambiguation sometimes requires to write $\mathcal{C}_{\mathscr{Z}}$, $\mathcal{R}_{\mathscr{Z}}$, and $\mathcal{U}_{\mathscr{Z}}$ rather than $\mathcal{C}$, $\mathcal{R}$, and $\mathcal{U}$ respectively.

In order to do static type checking, all concepts and relations must be "known" in the schema: $\begin{aligned} \text{\it n}_{\langle{A},{B}\rangle}\in\mathcal{R}&\Rightarrow&A\in\mathcal{C}\ \wedge\ B\in\mathcal{C}\\ \langle{a},{\text{\it n}_{\langle{A},{B}\rangle}},{b}\rangle\in\mathcal{T}&\Rightarrow&\text{\it n}_{\langle{A},{B}\rangle}\in\mathcal{R} \end{aligned}$

We say that a triple $\langle{a},{r},{b}\rangle$ befits schema $\langle{\mathcal{C}},{\mathcal{R}},{\mathcal{U}}\rangle$ if it satisfies these requirements.

A special kind of rule is used for specialization. The rule $A\preceq B$ (pronounce: $A$ is a $B$) states that any instance of $A$ is an instance of $B$ as well.

$\text{\it sat}_{A\preceq B}(\mathscr{D})\ \Leftrightarrow\ \forall a: a\ \text{\it inst}\ A\rightarrow a\ \text{\it inst}\ B$

This is called specialization, but it is also known as generalization or subtyping. You need specialization to allow statements such as: "An employee is a person" or "A human is a mammal". The specialization rules in a schema form a partial order $\preceq$, meaning that $\preceq$ is reflexive, transitive, and antisymmetric. Specialization rules are special for two reasons: Firstly, the system keeps $A\preceq B$ satisfied automatically by changing $\text{\it inst}$ whenever needed. This means that a system that contains rule $A\preceq B$ can never be brought into a state in which $\text{\it sat}_{A\preceq B}$ is False. This allows for certain run-time optimizations, which are beyond the scope of this paper. A second property that sets specialization rules apart, is that they play a role in the Ampersand compiler. For example, code that determines equality between atoms only works for atoms that are an instance of the same concept. To ensure that this does not result in problems at run-time, users are required to write all specialization rules explicitly.

As a result, if an atom is an instance of concept $A$ and $A\preceq B$, this atom has all properties that atoms of type $B$ have.

Information Systems

This section defines the notion of information system. As before, a suffix disambiguates the elements of this definition when needed.

Definition 1 (information system).

An information system $\mathscr{S}$ is a tuple $\langle\mathscr{D},\mathscr{Z},\mathcal{O},\text{\it maint}\rangle$, in which:

• dataset $\mathscr{D}=\langle{\mathcal{T}},{\text{\it inst}}\rangle$ as defined previously;

• schema $\mathscr{Z}=\langle{\mathcal{C}},{\mathcal{R}},{\mathcal{U}}\rangle$ as defined previously;

• $\mathcal{O}$ is a set of roles;

• $\text{\it maint}: \mathcal{O}\times\mathcal{U}$ is the maintainance relation between roles and rules.

A role is a name that identifies a group of users. It serves as a placeholder for a person or a machine (i.e. an actor) that works with the dataset (i.e. create, read, update, or delete triples). The purpose of a role is to mention an individual user (human) or an automated actor (bot) without knowing who that user is.

The system is at rest when every rule in the schema is satisfied:

$\forall u\in\mathcal{U}:\ \text{\it sat}_{u}(\mathscr{D})$

However, the system continually registers events that insert or delete triples in its dataset, which may cause rules to be broken. This requires a reaction to restore invariance. Example: if a rule says that every request must be acknowledged, the receipt of a request (which is an event) will violate this rule. Sending a message that acknowledges this receipt (another event) will cause the rule to be satisfied again. During the time between the receipt of the request and sending the acknowledgment, the rule is (temporarily) not satisfied.

Ampersand assumes two ways of enforcing satisfaction of rules: automatic or manual. Manual enforcement is specified by the developer by assigning a rule $u$ to a role $o$. Any actor with role $o$, whether person or machine, can restore invariance of rule $u$ by inserting or deleting the right triples. For this reason, every rule is assigned to at least one role by means of the relation $\text{\it maint}$:

$\forall u\in\mathcal{U}\ \exists o\in\mathcal{O}:\ o\ \text{\it maint}\ u$

$o\ \text{\it maint}\ u$ means that role $o$ must keep rule $u$ satisfied, i.e. to keep $\text{\it sat}_{u}(\mathscr{D})$ true. As long as rule $u$ is broken, the system should notify actors in the role(s) that are administered in $\text{\it maint}$ to do something about it.

Automatic enforcement is specified by the developer with a special syntax, the enforcement rule. An enforcement rule specifies not only the rule, but also the way to restore invariance. The system features an engine that restores invariance of all enforcement rules without unneccessary delay. Whenever the dataset violates an enforcement rule, this engine will make other changes to the dataset to satisfy that rule. Hence, the rule is not satisfied during a small, finite amount of time.

The system contains a dedicated role for the enforcement engine, so every rule has at least one role in the relation $\text{\it maint}$, means that all roles together are keeping all rules satisfied.

Example

Having defined an information system in mathematical terms, let us discuss a small example. It is written in the language Ampersand to make it more appealing to read. Let us first define a dataset of just a handful of triples and three relations.

RELATION takes[Student*Course] =
[ ("Peter", "Management")
; ("Susan", "Business IT")
; ("John", "Business IT")
]

This declaration introduces a relation with the name takes, source concept Student, and target concept Course. The informal meaning of this relation is that it states which students are taking which courses.

The example system also has a second relation that states which modules are part of which course.

RELATION isPartOf[Module*Course] =
[ ("Finance", "Management")
; ("Business Rules", "Business IT")
; ("Business Analytics", "Business IT")
; ("IT-Governance", "Management")
]

The third and last relation states which students are enrolled for which module. It is left empty for now.

RELATION isEnrolledFor[Student*Module]

A rule, EnrollRule completes the semantics It states that a student can enroll for any module that is part of a course he or she takes. In Ampersand, which is a syntactically sugared form of relation algebra [@JoostenRAMiCS2017], each rule has a name and each rule has a role to maintain its invariance:

RULE EnrollRule: isEnrolledFor |- takes;isPartOf~
ROLE Administrator MAINTAINS EnrollRule

The semantics of this rule defines $\text{\it sat}_{\tt EnrollRule}(\mathscr{D})$ as:

$\begin{aligned} \forall \langle{s},{m}\rangle\in\text{\it pop}_{\tt isEnrolledFor}(\mathscr{D})\ \exists c\in\text{\tt Course}:\\ s\ \text{\tt isEnrolledFor}\ m\ \rightarrow\ s\ \text{\tt takes}\ c\ \wedge\ m\ \text{\tt isPartOf}\ c \end{aligned}$

Rule EnrollRule is satisfied because relation $\text{\it \tt isEnrolledFor}_{\langle{\tt Student},{\tt Module}\rangle}$ is empty.

Now let us check the requirements to verify that this example defines an information system. The Ampersand compiler generates a dataset $\mathscr{D}$, which contains a set of triples and a relation $\text{\it inst}$. It defines the set of triples $\mathcal{T}$ as:

$$\begin{array}{llr} \langle{\text{\tt "Peter"}},&{\text{\it \text{\tt takes}}_{\langle{\text{\tt Student}},{\text{\tt Course}}\rangle}},&{\text{\tt "Management"}}\rangle\\ \langle{\text{\tt "Susan"}},&{\text{\it \text{\tt takes}}_{\langle{\text{\tt Student}},{\text{\tt Course}}\rangle}},&{\text{\tt "Business IT"}}\rangle\\ \langle{\text{\tt "John"}},&{\text{\it \text{\tt takes}}_{\langle{\text{\tt Student}},{\text{\tt Course}}\rangle}},&{\text{\tt "Business IT"}}\rangle\\ \langle{\text{\tt "Finance"}},&{\text{\it \text{\tt isPartOf}}_{\langle{\text{\tt Module}},{\text{\tt Course}}\rangle}},&{\text{\tt "Management"}}\rangle\\ \langle{\text{\tt "Business Rules"}},&{\text{\it \text{\tt isPartOf}}_{\langle{\text{\tt Module}},{\text{\tt Course}}\rangle}},&{\text{\tt "Business IT"}}\rangle\\ \langle{\text{\tt "Business Analytics"}},&{\text{\it \text{\tt isPartOf}}_{\langle{\text{\tt Module}},{\text{\tt Course}}\rangle}},&{\text{\tt "Business IT"}}\rangle\\ \langle{\text{\tt "IT-Governance"}},&{\text{\it \text{\tt isPartOf}}_{\langle{\text{\tt Module}},{\text{\tt Course}}\rangle}},&{\text{\tt "Management"}}\rangle \end{array}$$

The relation $\text{\it inst}$ contains the pairs:

$$\begin{array}{lcr} \langle{\tt "Finance"}&,&{\tt Module}\rangle\\ \langle{\tt "Business Rules"}&,&{\tt Module}\rangle\\ \langle{\tt "Business Analytics"}&,&{\tt Module}\rangle\\ \langle{\tt "IT-Governance"}&,&{\tt Module}\rangle\\ \langle{\tt "Management"}&,&{\tt Course}\rangle\\ \langle{\tt "Business IT"}&,&{\tt Course}\rangle\\ \langle{\tt "Peter"}&,&{\tt Student}\rangle\\ \langle{\tt "Susan"}&,&{\tt Student}\rangle\\ \langle{\tt "John"}&,&{\tt Student}\rangle \end{array}$$

The tuple $\langle{\mathcal{T}},{\text{\it inst}}\rangle$ is well-typed, so this is a dataset $\mathscr{D}$ as introduced before.

The Ampersand compiler generates a schema $\mathscr{Z}$, which contains concepts, relations and rules. It defines the set of concepts:

$\mathcal{C}=\{ {\tt Module}, {\tt Course}, {\tt Student}\}$

It defines the set of relations:

$$\begin{array}{ll} \mathcal{R}\ =\ \{&\text{\it \tt takes}_{\langle{\tt Student},{\tt Course}\rangle},\\ &\text{\it \tt isPartOf}_{\langle{\tt Module},{\tt Course}\rangle},\\ &\text{\it \tt isEnrolledFor}_{\langle{\tt Student},{\tt Module}\rangle}\ \} \end{array}$$

And, it defines the set of rules $\mathcal{U}$ to contain just one rule: EnrollRule. This example contains no specialization. So, the schema $\mathscr{Z}=\langle{\mathcal{C}},{\mathcal{R}},{\mathcal{U}}\rangle$ satisfies all requirements mentioned above.

Now let us check the definition of information system. Ampersand generates a set of roles $\mathcal{O}=\{{\tt Administrator}\}$. The relation $\text{\it maint}$ contains one pair only, $\langle{{\tt Administrator}},{{\tt EnrollRule}}\rangle$, instructing the run-time engine to forward all violations of EnrollRule to an administrator so she can keep EnrollRule satisfied. We can see that the only rule, EnrollRule, is satisfied, which completes the requirements for $\mathscr{S}=\langle\mathscr{D},\mathscr{Z},\mathcal{O},\text{\it maint}\rangle$. This concludes the argument that $\mathscr{S}$ is an information system.

Relation to other theories

The following table compares the language used in the world of information systems with related worlds. It is compared with Ampersand, because we use Ampersand to design information systems. It is compared with the world of software, because Ampersand generates software. It is compared with the world of model theory [ref required], because the formal theory of Ampersand can be understood formally in model theory.

information system	Ampersand	software	model theory
rules	script	program	theory
data	population	state	model
formal statement	term	condition	term
generator	generator	compiler
store	database	database
interface	interface	interface

The following theoretical topics are relevant for Ampersand.

1. Relation Algebra [Maddux 2006] Ampersand uses heterogeneous relation algebras with specialization as a language to specify information systems. This is existing theory. It is relevant for people who specify information systems. It allows them to formalize business rules. Thus, they can ensure on design time that an information system complies with business rules.

2. Rewrite systems The Ampersand compiler manipulates relation algebra terms. For this purpose, it uses rewrite systems. This is existing theory. It is relevant for people who make the Ampersand-compiler generate efficient code.

3. Type systems The Ampersand compiler ensures that every type-correct specification can be built [1]. For this purpose it has a type system, which signals type-errors in Ampersand-scripts. The Ampersand-compiler generates code only for scripts without type errors.

4. Generating computations It is possible to generate code to keep constraints satisfied. The theory for this is under development. It is relevant for automating tasks in information systems.

5. Compiler theory Ampersand is a compiler. Its syntax is parsed by the Parsec-module of Haskell. A hand-written generator embodies the semantics. The theory is existing. This subject is relevant for people who wish to change the language of Ampersand.

Each of the following sections treats on of the topics mentioned above (work to be done).

[1] Michels, G., Joosten, S., van der Woude, J., Joosten, S.: Ampersand: ApplyingRelation Algebra in Practice. In: de Swart, H. (ed.) RAMICS 2011. LNCS, vol. 6663,pp. 280–293. Springer, Heidelberg (2011)